Абсолютная температура идеального газа. Формулы. Пример задачи

Температура - термодинамическая макроскопическая характеристика, которая играет важную роль практически во всех физических процессах. В данной статье сосредоточим свое внимание на освещении вопросов, что такое абсолютная температура газа идеального и как ее можно вычислить.

Абсолютная шкала температур

Для начала познакомимся со шкалой, которая используется в физике для описания температуры. Она называется абсолютной или шкалой Кельвина. Впервые ее ввел в использование английский физик лорд Кельвин в 1848 году. При этом ученый основывался на завоевавшей популярность шкале Цельсия.

Абсолютная температура так называется потому, что она имеет нижний предел - 0 кельвин, при котором считается "замороженным" любой вид движения (на самом деле при 0 К существуют так называемые нулевые колебания). Верхнего предела у этой шкалы нет.

С градусами Цельсия C абсолютная шкала T связана следующим простым равенством:

T = C + 273,15.

В отличие от других температурных шкал, например, от шкалы Фаренгейта, кельвин имеет точно такой же масштаб, что и градус Цельсия. Последнее означает, что для перевода в абсолютную любой температуры по Цельсию достаточно добавить к ней число 273,15. Так, по шкале Кельвина вода замерзает при 273,15 К, а кипит при 373,15 К.

Краткое понятие о газе идеальном

Поскольку далее будет рассмотрена формула для определения абсолютной температуры газа идеального, то будет полезным познакомиться с этим понятием поближе. Под идеальным понимают такой газ, молекулы которого практически не взаимодействуют друг с другом, обладают большой кинетической энергией по сравнению с потенциальной, и расстояния между которыми значительно превышают их собственные размеры.

Все реальные газы проявляют поведение идеальных при небольших давлениях и высоких температурах. Примерами могут служить благородные газы, воздух, метан и другие. В то же время пар H2O даже при низких давлениях сильно отличается от идеального газа, поскольку в нем всегда присутствуют значительные водородные связи между полярными молекулами воды.

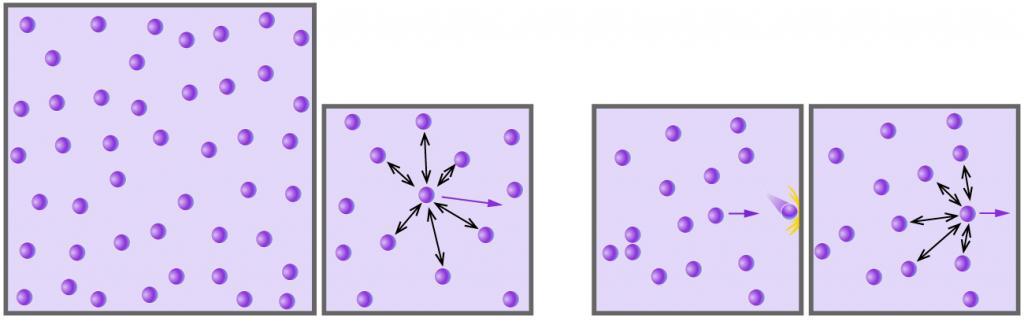
Температура абсолютная идеального газа

Существует два подхода к определению температуры в газах. Рассмотрим каждый из них.

Первый подход заключается в привлечении положений молекулярно-кинетической теории (МКТ) и физического смысла самой температуры T. Последний заключается в кинетической энергии частиц газа. Чем больше эта энергия, тем выше температура, причем зависимость является прямо пропорциональной. Используя формулу из механики для энергии кинетической и постоянную Больцмана kB можно записать следующее равенство МКТ:

m*v2/2 = 3/2*kB*T.

Где m - масса движущейся поступательно частицы. Выражая из этого равенства величину T, получаем формулу:

T = m*v2/(3*kB).

Чем меньше масса частицы и чем больше ее скорость, тем выше абсолютная температура.

Второй подход в определении величины T заключается в использовании универсального уравнения Клапейрона-Менделеева. Это уравнение было записано в XIX веке Эмилем Клапейроном (впоследствии модифицировано Д. И. Менделеевым) как результат обобщения открытых экспериментально в XVII-XIX веках газовых законов (Шарля, Гей-Люссака, Бойля-Мариотта, Авогадро). Математически универсальное уравнение записывается так:

P*V = n*R*T.

Как видно, оно связывает три основных термодинамических величины системы: давление P, объем V и температуру абсолютную T. Две другие величины, присутствующие в уравнении, - это n - количество вещества и R - газовая постоянная.

Не представляет особого труда получить формулу для температуры из Клапейрона-Менделеева закона:

T = P*V/(n*R).

В закрытой системе (n = const) температура газа прямо пропорциональна произведению объема на давление.

Пример задачи

Воздух, которым мы дышим, является смесью газов идеальных. Известно, что молярная масса воздуха составляет 29 г/моль. Необходимо определить температуру воздуха, если средняя скорость его молекул составляет 530 м/с.

Очевидно, что решение этой задачи можно получить, если воспользоваться следующим выражением:

T = m*v2/(3*kB).

Массу одной молекулы m воздуха можно получить, если поделить величину M на число Авогадро NA. Произведение же числа NA на константу Больцмана kB - это не что иное, как газовая постоянная R, которая равна 8,314 Дж/(К*моль). Учитывая эти рассуждения, получаем рабочую формулу:

T = M*v2/(3*R ) = 0,029*6002/(3*8,314) = 326,60 К.

В градусах Цельсия найденной температуре соответствует значение 53,45 oC. На нашей планете такие температуры характерны для жарких песчаных пустынь в полдень.