В физике закон Гаусса о потоке вектора напряженности электрического поля является правилом, связывающим распределение зарядов. Рассматриваемая поверхность может быть закрытой, охватывающей объем, такой, как сферическая поверхность.
Впервые закон был сформулирован Жозефом-Луи Лагранжем в 1773 году, а затем Карлом Фридрихом Гауссом в 1813 году в контексте притяжения эллипсоидов. Это одно из четырех уравнений Максвелла, лежащих в основе классической электродинамики. Закон Гаусса можно использовать для вывода закона Кулона и наоборот.
Математический аспект
Закон Гаусса имеет математическое сходство с рядом законов в других областях физики, таких, как теории магнетизма и гравитации. Фактически, любой закон обратных квадратов можно сформулировать аналогично закону Гаусса. Например, он сам по существу эквивалентен закону Кулона обратного квадрата.
Закон может быть выражен математически с использованием векторного исчисления в интегральной форме и дифференциальной форме; оба эквивалентны, так как они связаны теоремой расходимости, также называемой теоремой Гаусса. Каждая из этих форм, в свою очередь, также может быть выражена двумя способами: в терминах зависимости между электрическим полем E и полным электрическим зарядом или в терминах поля электрического смещения D и свободного электрического заряда.
Интегрирование
Если электрическое поле известно повсеместно, закон Гаусса позволяет найти распределение электрического заряда: заряд в любой данной области может быть выведен путем интегрирования электрического поля, чтобы найти поток вектора напряженности электрического поля.
Обратная задача (когда распределение электрического заряда известно и электрическое поле должно быть вычислено) гораздо сложнее. Общий поток вектора напряженности электрического поля через данную поверхность дает мало информации об электрическом поле и может входить и выходить из поверхности в произвольно сложных схемах.
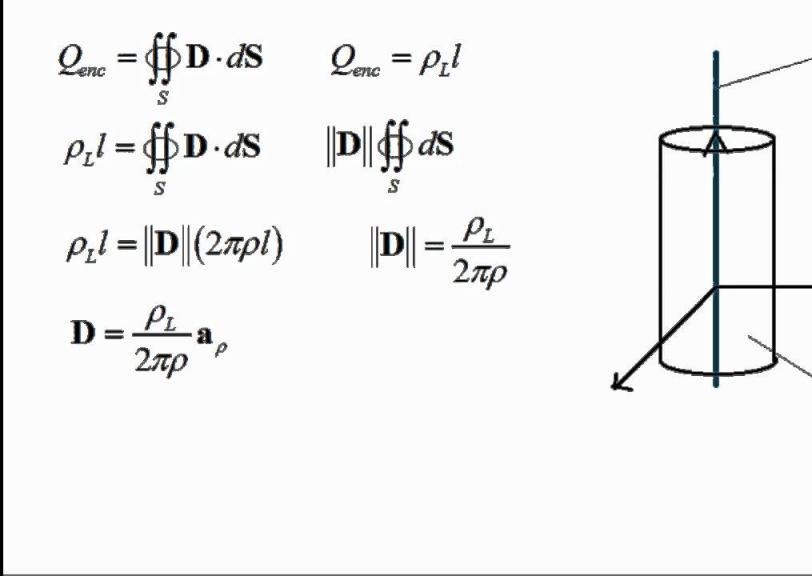
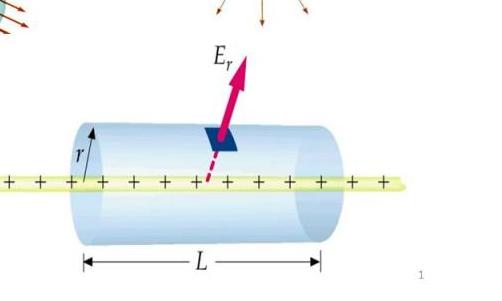
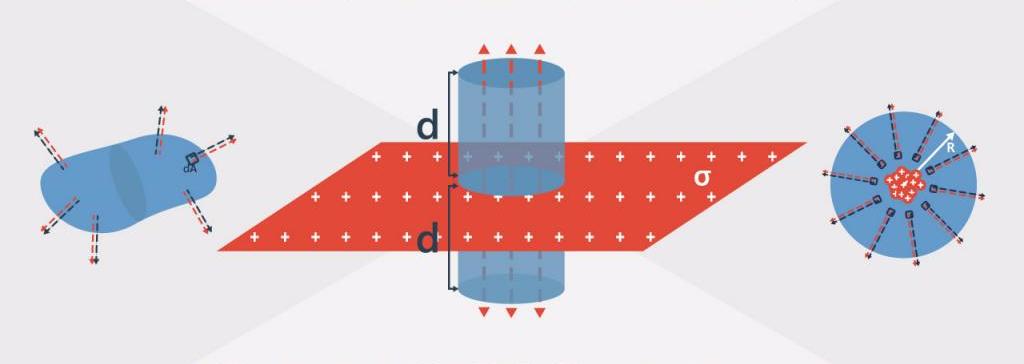
Исключением является наличие некоторой симметрии в задаче, которая требует, чтобы электрическое поле проходило через поверхность равномерным образом. Если общий поток вектора напряженности электрического поля известен, само поле может быть выведено в каждой точке. Общие примеры симметрий, которые поддаются закону Гаусса, включают цилиндрическую симметрию, плоскую симметрию и сферическую симметрию.
Свободный заряд
Электрический заряд, который возникает в простейших ситуациях из учебника, будет классифицироваться как «свободный заряд», например, заряд, который переносится статическим электричеством или заряд на пластине конденсатора. Напротив, «связанный заряд» возникает только в контексте диэлектрических (поляризуемых) материалов. (Все материалы в некоторой степени поляризуемы.) Когда такие материалы помещаются во внешнее электрическое поле, электроны остаются связанными со своими соответствующими атомами, но смещают микроскопическое расстояние в ответ на поле, так что они больше на одной стороне атома, чем на другой. Все эти микроскопические смещения в сумме дают макроскопическое распределение чистого заряда, что составляет «связанный заряд».
Хотя микроскопически весь заряд в основном одинаков, часто существуют практические причины желать рассматривать связанный заряд иначе, чем свободный заряд. Результатом является то, что более фундаментальный закон Гаусса в терминах E (выше) иногда приводится в эквивалентной форме ниже, то есть в терминах D и только свободного заряда.
Силовые линии
Закон Гаусса может быть истолкован в терминах силовых линий поля следующим образом.
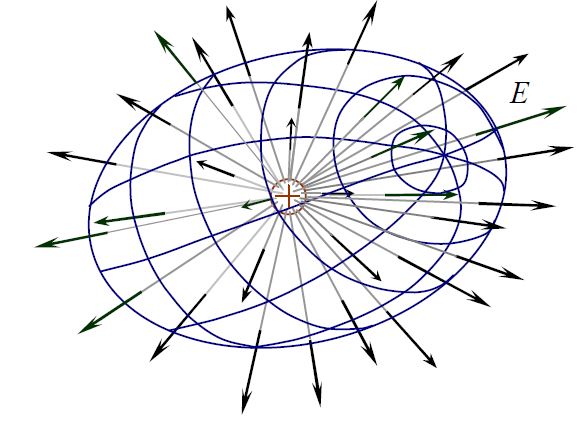
Поток вектора напряженности электрического поля через поверхность зависит как от его величины, так и от направления его линий. В общем случае положительный поток определяется этими линиями, выходящими из поверхности, а отрицательный - линиями, входящими в эту поверхность. Это приводит к тому, что положительные заряды вызывают положительный отклик, а отрицательные заряды создают отрицательный. Эти линии электрического поля будут бесконечно уменьшаться по силе на единицу на расстоянии от источника квадрата заряда. Чем больше число силовых линий, исходящих от заряда, тем больше величина заряда, и чем ближе друг к другу силовые линии, тем больше величина электрического поля.
Это естественный результат того, что электрическое поле становится слабее по мере удаления от заряженной частицы, но площадь поверхности также увеличивается, так что суммарное электрическое поле, выходящее из этой частицы, останется прежним. Другими словами, замкнутый интеграл электрического поля и скалярное произведение производной площади будут равны приложенному суммарному заряду, деленному на диэлектрическую проницаемость свободного пространства.
Отличия
Строго говоря, закон Гаусса не может быть выведен из одного закона Кулона, поскольку закон Кулона дает электрическое поле только за счет отдельного точечного заряда. Однако закон Гаусса может быть доказан из закона Кулона, если, кроме того, предполагается, что электрическое поле подчиняется принципу суперпозиции. Принцип суперпозиции гласит, что результирующее поле является векторной суммой полей, генерируемых каждой частицей (или интегралом, если заряды равномерно распределены в пространстве).
Обратите внимание, что поскольку закон Кулона применяется только к стационарным зарядам, нет никаких оснований ожидать, что закон Гаусса будет действовать для движущихся зарядов, основываясь только на этом выводе. Фактически, закон Гаусса на самом деле действует для движущихся зарядов, и в этом отношении закон Гаусса является более общим, чем закон Кулона.
Строго говоря, закон Кулона не может быть выведен из одного закона Гаусса, поскольку закон Гаусса не дает никакой информации относительно скручивания E (см. "Разложение Гельмгольца и закон Фарадея"). Тем не менее, закон Кулона может быть доказан из закона Гаусса, если предположить, что электрическое поле от точечного заряда сферически симметрично (это предположение, как и сам закон Кулона, точно верно, если заряд является стационарным, и приблизительно верно, если заряд находится в движении).
Примеры и визуализация
Электрическое поле является векторным полем, величина и направление которого определено в каждой точке пространства. Другим примером векторного поля, которое легче визуализировать, является скорость воды в потоке вектора напряженности через замкнутую поверхность. Это величина того, что поле представляет, проходя через область. Общий поток вектора напряженности электростатического поля в вакууме зависит от напряженности поля, размера площади поверхности, через которую он проходит, и от того, как область ориентирована относительно поля. Вы можете думать о нем как о количестве чего-то, пересекающего поверхность.
Поверхность представляет собой двумерную (реальную или воображаемую) границу, может быть открытой или закрытой. Открытая поверхность может быть областью двери, областью листа бумаги, областью чаши и т. д. Закрытой поверхностью может быть поверхность из сферы или куба и т. д. Как нам убедительно доказывает теорема Остроградского-Гаусса, поток вектора напряженности измеряется в единый момент времени. Поток - это общее количество чего-либо, пересекающего поверхность, но это не что-то на единицу площади и т. д.
Максимальное количество линий поля перехватывается, когда единичный вектор, нормальный к поверхности, n, параллелен полю E, в то время, как никакие линии поля не проходят через поверхность, когда n перпендикулярно полю. Число линий поля, проходящих через область A, прямо пропорционально A * cosθ, где θ - угол между направлением поля и единичным вектором n, перпендикулярным поверхности. Это приводит к определению электрического потока.
ΔΦE - электрический поток через некоторую небольшую область ΔA, нормаль которой составляет угол θ с направлением электрического поля. Е - это величина поля. Единица СИ потока - Нм2 / с. Это и есть ответ на вопрос, в чем измеряется поток вектора напряженности.
Область E
E - векторная величина. Полезно также представлять область A вектором A. Длина этого вектора равна размеру области, а ее ориентация перпендикулярна области. Это в направлении нормального п. У нас есть A = An. Нормаль к поверхности может указывать в двух разных направлениях. Для замкнутой поверхности условно нормаль указывает наружу. С нашим определением A мы можем записать формулу потока вектора напряженности в виде точечного произведения E и ΔA.
Сигнал через какую-либо поверхность может быть положительным или отрицательным, поскольку косинус может быть положительным или отрицательным. Поток через закрытую поверхность является положительным, если есть чистый внешний поток, и отрицательным, если есть чистый внутренний поток. У нас есть чистый поток наружу, если внутри замкнутой поверхности есть источник, и чистый поток внутрь, если внутри замкнутой поверхности есть сток.
Кубическая поверхность
Рассмотрим электрический поток, проходящий через кубическую поверхность с двумя его гранями, перпендикулярными однородному электрическому полю. Поток, проходящий через верхнюю, нижнюю, переднюю и заднюю стороны куба, равен нулю, поскольку эти стороны параллельны полевым линиям и, следовательно, не пересекают ни одну из них. Вектор нормали n перпендикулярен полю для этих сторон, и cosθ равен нулю. Как показано, линии поля параллельны вектору нормали n для правой стороны, поэтому поток через эту сторону равен ΦE = EA. Линии поля антипараллельны вектору нормали n для левой стороны, поэтому поток через эту сторону равен ΦE = -EA. Общий поток через поверхность куба является суммой потоков через все стороны и равен нулю.
Поток векторного поля через замкнутую поверхность всегда равен нулю, если в объеме, окруженном поверхностью, нет источника или поглотителя векторного поля. Источниками и поглотителями электрического поля являются заряды.
Радиус R
Представьте себе сферу радиуса R с равномерно распределенным внутри зарядом. Симметрия распределения заряда требует сферически-симметричного электрического поля. Поле должно быть направлено радиально внутрь к центру или наружу от центра сферы. Если у нас сферически-симметричное распределение заряда, то, независимо от того, как мы ориентируем нашу систему координат, распределение всегда выглядит одинаково. Поэтому поле должно также выглядеть одинаково, независимо от того, как мы ориентируем нашу систему координат. Поле, которое не радиальное, будет выглядеть иначе, если мы повернем нашу систему координат, т. е. если мы посмотрим на нее под другим углом.
Поэтому для сферического симметричного распределения заряда величина E может зависеть только от радиальной координаты r и заряда Q. Чтобы определить E как функцию от r, мы используем закон Гаусса. Нарисуем сферическую гауссову поверхность радиуса r с центром в центре сферического распределения заряда. Радиус r поверхности может быть больше или меньше радиуса R распределения.
Закон Гаусса - одно из двух утверждений, описывающих электрические и магнитные потоки. Закон Гаусса об электричестве гласит, что электрический поток через любую замкнутую поверхность пропорционален суммарному электрическому заряду, приложенному поверхностью. Закон подразумевает, что существуют изолированные электрические заряды, и что подобно зарядам, они отталкиваются друг от друга, а в отличие от зарядов, притягиваются.
Закон Гаусса о магнетизме гласит, что магнитный поток через любую замкнутую поверхность равен нулю; этот закон согласуется с наблюдением, что изолированные магнитные полюсы (монополи) не существуют.
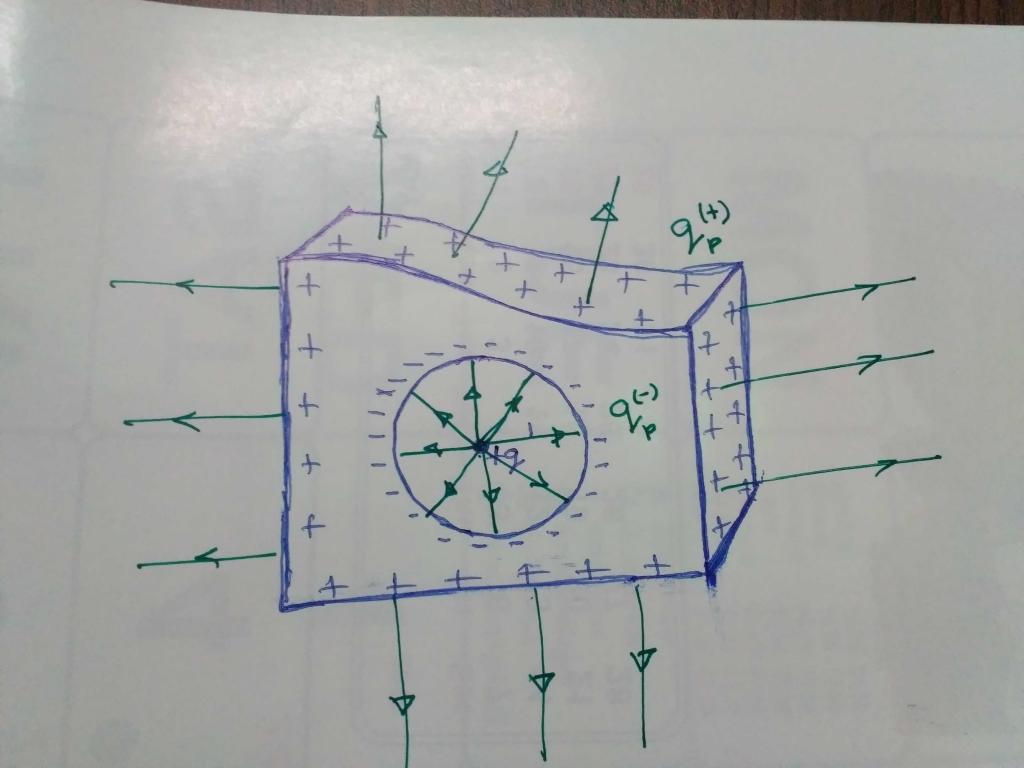
Математические формулировки
Математические формулировки для этих двух законов - вместе с законом Ампера (относительно магнитного эффекта изменения электрического поля или тока) и законом индукции Фарадея (относительно электрического эффекта изменения магнитного поля) - собраны в наборе, который известен как Уравнения Максвелла (см.). Они составляют основу единой электромагнитной теории.
Связи
Связь между векторными полями в физике и их источниками, например, между гравитационным полем и массами, между электрическим полем и электрическими зарядами, а также между магнитным полем и магнитными диполями можно выразить удивительно простым и элегантным образом, известным как закон Гаусса. С практической точки зрения закон Гаусса часто полезен при определении полного электрического или гравитационного поля, возникающего из распределений зарядов или масс, которые имеют достаточную симметрию.
В этих ситуациях часто проще использовать закон Гаусса, чем складывать все вклады в общее поле, приходящиеся на каждую отдельную часть заряда или распределения массы.
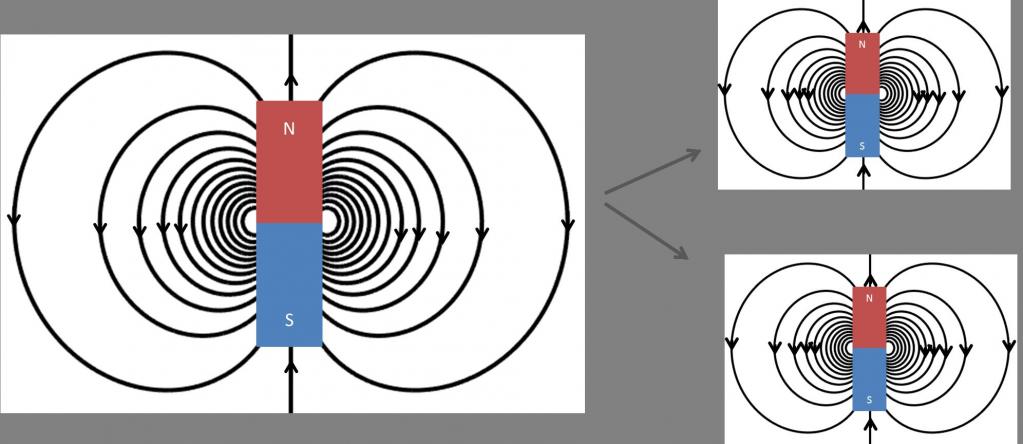
Векторные потоки
Закон Гаусса включает в себя величину, называемую потоком (также известным как интегральный поток или полный поток) электрического, гравитационного или магнитного поля из воображаемой двумерной поверхности, когда эта поверхность является непосредственной границей трехмерного объема. Рассматриваемая двумерная поверхность должна рассматриваться как «нарисованная в пространстве», то есть это чисто математическая конструкция, которую не следует путать с любой материальной поверхностью, которая может быть частью физической ситуации.
Например, вы можете представить трехмерную часть пространства в форме шара, и рассматриваемая поверхность будет его граничной поверхностью, которая является сферой.
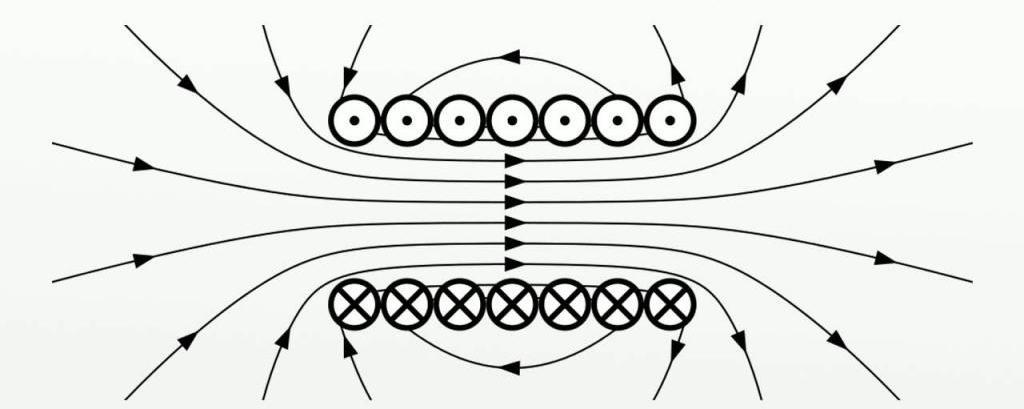
Грубо говоря, теорема Гаусса гласит, что при произвольной такой двумерной поверхности, если суммировать нормальные компоненты поля по всей поверхности, результат, пропорциональный суммарному заряду, приложенному поверхностью, то есть заряду, присутствующему в части пространства, границей которой является поверхность.
Заключение
Концепция потока является важной и распространенной в физике. В случае веществ или энергии, которые физически протекают через пространство и, в частности, через данную поверхность, поток относится к скорости потока (вещества или энергии) через поверхность. Но можно определить поток вектора напряженности через поверхность, даже если, как и в случае электрического, гравитационного или магнитного поля, векторное поле не описывает поток какого-либо физического объекта.

























А ЧТО ВЫ ДУМАЕТЕ ОБ ЭТОМ?