
Немногие знают, как решить данный математический пример: 6:2(1+2)=? По всей видимости, эта «простая» математическая операция не имеет особых трудностей. Но почему же она сводит с ума пользователей Интернета? Здесь присутствуют небольшие числа, есть деление, умножение и сумма. Так почему же решение примера так проблематично? Выясним это ниже.
Разные результаты

Если вы уже пытались решить вышеуказанный пример, вы, вероятно, получили два результата: 1 или 9.
Несколько раз в соцсетях распространялись простые арифметические расчеты, которые вызывают споры среди пользователей. Ведь не все приходят к одному и тому же решению. Почему при выполнении одной и той же операции появляются разные результаты?
Ключ к решению
Итак, вы должны начать решать пример справа налево. Сперва выполняются действия в скобках. Затем нужно приступать к умножению и делению. Следом идет сложение и вычитание. Вы должны запомнить этот порядок. Тогда вы сможете решить спорный пример.
Пошаговое решение

Первый шаг – решите то, что находится в скобках. В нашем случае мы имеем (1+2), следовательно, ответ будет 3. Пример теперь будет выглядеть так: 6:2(3).
Дальше приходит сомнение: нужно делить или умножать? Обе операции имеют одинаковый уровень приоритета.
Второй шаг выглядит так. Мы выполняем операцию двумя способами:
- Выполняем умножение: 2 Х 3 = 6. После реализуем последнюю операцию: 6 : 6 = 1.
- Реализуем деление: 6 : 2 = 3. После выполняем умножение: 3 Х 3 = 9.
1 или 9?
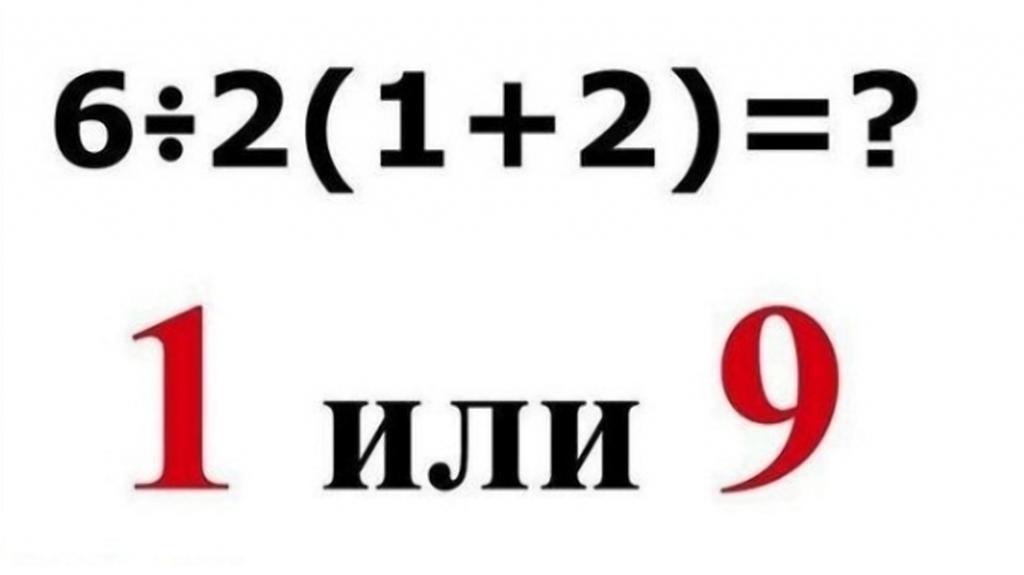
Математика не является субъективным вопросом. Каждый знает, что 1 + 1 = 2. Так какой же ответ правильный?
Дискуссия закрыта: оба варианта верны. Дэвид Линклеттер, умелый математик, в своей статье «Пародокс ПЕНДАС» говорит, что существует две немного разные интерпретации папомуд. Результат зависит от того, как вас учили, и, как правило, ни один из вариантов не превалирует над другим.
Некоторых учили, что 2(3) равно 2 Х 3, поэтому операция будет выглядеть так: 6 : 2 Х 3. И, если решать справа налево, результат будет 9.
Тем не менее, другие учили, что 2(3) – это то же самое, что (2 Х 3). Так что умножение будет выполнено перед делением. Далее операция будет реализована как 6 : 6, давая в качестве конечного результата 1.
Линклеттер объясняет, что математически противоречиво полагать, что a (b) взаимозаменяемо с axby, а а (b) взаимозаменяемо с (ab) потому, что тогда следует, что 1 = 9.
В подобных случаях эксперты предлагают окончательный ответ. Однако на этот раз кажется маловероятным, что пример решен. Ведь это не чисто математическая проблема, а вопрос коммуникации.
Как упоминалось выше, оба варианта одинаково популярны, поэтому одно из решений не может быть навязано, имея большее количество последователей.
Теперь вы знаете, что можете продолжать защищать свой способ решения этого типа операций. Но если вы говорите, что один из них неверный, то ошибаетесь как раз вы.

























А ЧТО ВЫ ДУМАЕТЕ ОБ ЭТОМ?